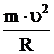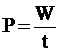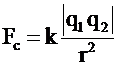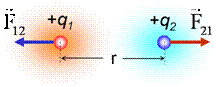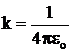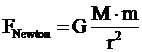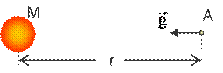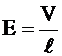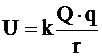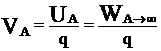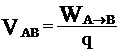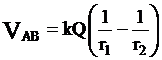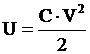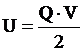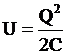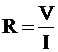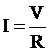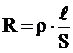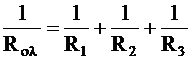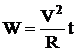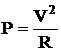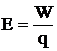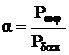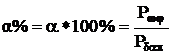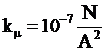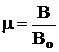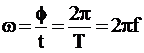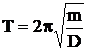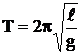ΤΥΠΟΙ - ΣΧΕΣΕΙΣ - ΦΥΣΙΚΟΙ ΝΟΜΟΙ

x = υ t				στην ευθύγραμμη ομαλή κίνηση το διάστημα x που διανύει το κινητό σε χρόνο t είναι ανάλογο της ταχύτητας υ (σταθ.).
x = υo t ± ½ α t^2 υ = υo ± α t				στην ευθύγραμμη ομαλά μεταβαλλόμενη (επιταχυνόμενη ή επιβραδυνόμενη κίνηση) υ η ταχύτητα που απέκτησε το κινητό αφού διήνησε απόσταση (διάστημα) x σε χρόνο t με αρχική ταχύτητα υo και σταθερή επιτάχυνση α
s = υ t ή φ = ω t υ = ω R ω = 2 π f = ακ = = ω^2 R				στην κυκλική ομαλή κίνηση s το τόξο (διάστημα) και φ η γωνία που διήνησε το κινητό σε χρόνο t, με γραμμική ταχύτητα υ και ω η γωνιακή ταχύτητα. R η ακτίνα περιστροφής, f η συχνότητα και Τ η περίοδος και ακ η κεντρομόλος επιτάχυνση του κινητού.
Fk = m ακ = = m ω^2 R				στην κυκλική ομαλή κίνηση που εκτελεί σώμα μάζας m ασκείται η κεντρομόλος δύναμη Fk (απο το σώμα προς το κέντρο).
W = F S συνφ				όπου W το έργο που παράγει δύναμη F σταθερή κατά μέτρο, διεύθυνση και φορά, S η μετατόπιση του σημείου εφαρμογής της και φ η γωνία που σχηματίζουν η διεύθυνση της δύναμης και της μετατόπισης.
				όπου Ρ η ισχύς δύναμης (ή μηχανής) που παράγει έργο W σε χρόνο t.
U = m g h				όπου U η δυναμική ενέργεια σώματος μάζας m που βρίσκεται σε ύψος h απο το επίπεδο αναφοράς (του οποίου η U = 0.) (g = 9,81 m/sec^2 η επιτάχυνση της βαρύτητας).
K = ½ m υ^2				K η κινητική ενέργεια του σώματος που κινείται με ταχύτητα υ.
Eμηχ = U + K				Εμηχ η μηχανική ενέργεια του σώματος
Τ = μ Fκ				όπου Τ η τριβή ολίσθησης που αναπτύσσεται σε σώμα Α που ολισθαίνει πάνω σε άλλο σώμα Β, μ ο συντελεστής τριβής ολίσθησης και Fκ η δύναμη που ασκεί η μία τριβόμενη επιφάνεια κάθετα πάνω στην άλλη.
1^ο κεφ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ
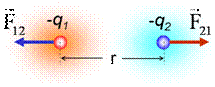
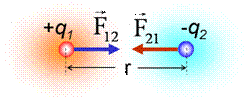
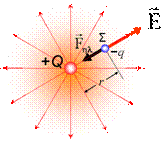
k=9^.10^9 N^.m^2/C^2			Νόμος Coulomb: Το μέτρο της δύναμης Fc που ασκεί ένα (σημειακό) φορτίο q1 σε ένα άλλο φορτίο q2, και r η απόσταση των δύο φορτίων. (όπου k ηλεκτρική σταθερά) όπου εo η απόλυτη διηλεκτρική σταθερά του κενού , (εο = 8,85 10^12 C^2/Nt m^2 )
			Νόμος (Δύναμη) Παγκόσμιας έλξης Μ μάζα Γης
(μέτρο)			Ένταση Βαρυτικού πεδίου Γης σε ύψος h από την επιφάνειά της, στο σημείο Α: όπου r = RΓ + h
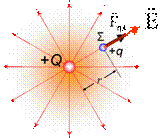
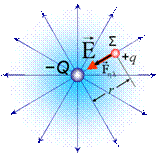
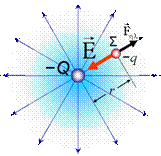
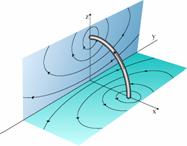
(μέτρο)			όπου Ε η ένταση ηλεκτρικού πεδίου στο σημείο Σ σε απόσταση r απο το (σημειακό) φορτίο Q το οποίο δημιουργεί το πεδίο Coulomb. Η Ε είναι ανεξάρτητη απο το φορτίο q.
Ισχύει:			ΔU = -WF(1→2) Uτελ(2) - Uαρχ(1) = -WF(1→2)
όπου Ε η ένταση ομογενούς ηλεκτροστατικού πεδίου το οποίο δημιουργούν δύο παράλληλες πλάκες που απέχουν απόσταση ℓ και έχουν διαφορά δυναμικού V.
			Ηλεκτρική δυναμική ενέργεια συστήματος δυο φορτίων
			Δυναμικό σε μία θέση (Α) ηλεκτρικού πεδίου
			Δυναμικό ηλεκτροστατικού πεδίου Coulomb
			Διαφορά Δυναμικού
			Διαφορά Δυναμικού ηλεκτροστατικού πεδίου Coulomb
			όπου C η χωρητικότητα πυκνωτή, Q το φορτίο του πυκνωτή όταν φορτίζεται και V το δυναμικό που αποκτά μεταξύ των οπλισμών του.
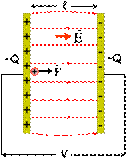
			όπου C η χωρητικότητα επίπεδου πυκνωτή κάθε οπλισμός του οποίου έχει εμβαδό S, ℓ η απόσταση των οπλισμών του, ε η σχετική διηλεκτρική σταθερά του υλικού που υπάρχει στο εσωτερικό του και εo η απόλυτη διηλεκτρική σταθερά.
			όπου U η ηλεκτρική δυναμική ενέργεια (ομογενούς ηλεκτροστατικού πεδίου) που έχει αποταμιευτεί σε πυκνωτή χωρητικότητας C, και Q το φορτίο το οποίο έχει ένας απο τους οπλισμούς του, και V η τάση που υπάρχει μεταξύ των οπλισμών του.
2^ο κεφ ΣΥΝΕΧΕΣ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ
		όπου Ι η ένταση ηλεκτρικού ρεύματος και q το ηλεκτρικό φορτίο που περνά από μιά φανταστική τομή του αγωγού σε χρόνο t.
		1^ος κανόνας Kirchhoff
		Αντίσταση αγωγού
, →V = I·R με R = σταθ		νόμος του OHM: η ένταση ηλεκτρικού ρεύματος I που διαρρέει αγωγό αντίστασης R, είναι ανάλογη της τάσης V που εφαρμόζεται στα άκρα του.
		όπου R η αντίσταση αγωγού μήκους ℓ και εμβαδού τομής S, ρ η ειδική αντίσταση του υλικού του αγωγού. (Παράγοντες από τους οποίους εξαρτάται η αντίσταση ενός αντιστάτη)
ρθ = ρο (1+αθ)		Ειδική αντίσταση
Rθ = Rο (1+αθ)		η αντίσταση ενός αντιστάτη εξαρτάται από την θερμοκρασία
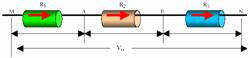
Vολ = V1 + V2 + V3 Iολ = I1 = I2 = I3 Rολ = R1 + R2 + R3		Σύνδεση αντιστάσεων σε σειρά
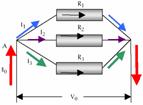
Ιολ = Ι1 + Ι2 + Ι3 Vολ = V1 = V2 = V3		Σύνδεση παράλληλα
Wηλ = V I t W=I^2Rt		όπου Wηλ η (ηλεκτρική) ενέργεια που παράγει πηγή τάσης V όταν στο κύκλωμα αναπτύσσει ηλεκτρικό ρεύμα έντασης I, και θερμότητα Q στην αντίσταση R, σε χρόνο t.
Q = I^2R t		Νόμος του Joule
, P=VI ,		Ισχύς ηλεκτρικού ρεύματος
,		ΗΕΔ πηγής
		Νόμος του Ohm για κλειστό κύκλωμα
Vπ =Ε-Ir		Πολική τάση πηγής
		Ρεύμα βραχυκύκλωσης
		Συντελεστής απόδοσης αποδέκτη
		Απόδοση αποδέκτη
3^ο κεφ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ
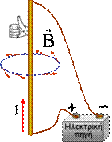
	νόμος των Μπιό και Σαβάρ (Biot-Savart): Ενα στοιχειώδες τμήμα Δℓ αγωγού που διαρρέεται απο ρεύμα έντασης Ι δημιουργεί σε τυχόν σημείο του χώρου, που απέχει απόσταση r απο το στοιχειώδες τμήμα Δℓ μαγνητικό πεδίο έντασης ΔΒ. Το θ είναι η γωνία που σχηματίζουν τα Δℓ και r. Το μo= 4π·10^-7V·sec/A·m = 4π·10^-7T·m/A η μαγνητική διαπερατότητα του κενού ή του αέρα.
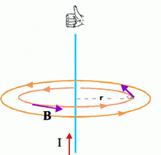
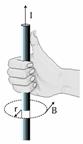
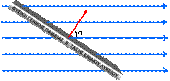
	Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού όπου Β η ένταση του μαγνητικού πεδίου σε απόσταση r απο ευθύγραμμο αγωγό απείρου μήκους που διαρρέεται απο ρεύμα έντασης I (και μo η μαγνητική διαπερατότητα του κενού ή του αέρα.)
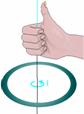
	Μαγνητικό πεδίο κυκλικού ρευματοφόρου αγωγού στο κέντρο του (με Ν αγωγούς) όπου Β το μέτρο της έντασης μαγνητικού πεδίου κυκλικού αγωγού ακτίνας r που διαρρέεται απο ρεύμα I
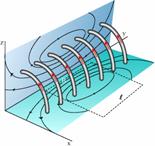
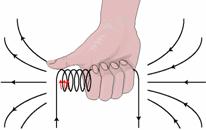
kμ = 10^-7	Μαγνητικό πεδίο σωληνοειδούς στο εσωτερικό του και κοντά στο κέντρο του όπου Β η ένταση του μαγνητικού πεδίου στο εσωτερικό πηνίου που έχει Ν σπείρες, μήκος ℓ και διαρρέεται απο ρεύμα έντασης I. Β΄ κοντά στα άκρα του
FL =BIℓ ημφ	Δύναμη Laplace
	Ορισμός της έντασης ομογενούς μαγνητικού πεδίου
μ >>1 μ > 1 μ < 1	Μαγνητική διαπερατότητα υλικού Σιδηρομαγνητικά υλικά Παραμαγνητικά υλικά Διαμαγνητικά υλικά
	Μαγνητικό πεδίο σωληνοειδούς με πυρήνα στο εσωτερικό του
Φ=ΒSσυνα 1Wb = 1 Τ·m^2 φ = 0° έχουμε Φ = B·S φ = 90° έχουμε Φ = 0 0° < φ < 90° Φ = Β·S·συνφ > 0 90° <φ<180° Φ = Β·S· συνφ<0	Μαγνητική ροή
	Νόμος επαγωγής Faraday Η επαγωγική ηλεκτρεγερτική δύναμη (τάση - Volt) που αναπτύσσεται σε ένα κύκλωμα είναι ανάλογη προς το ρυθμό μεταβολής της μαγνητικής ροής που περνά από αυτό το κύκλωμα. To Ν είναι ο αριθμός των σπειρών σε σωληνοειδές ή κυκλικό αγωγό.
	Επαγωγικό ρεύμα Κανόνας Lenz .To επαγωγικό ρεύμα έχει τέτοια φορά ώστε το αποτέλεσμα του να αντιστέκεται στο αίτιο που το προκαλεί.
	Νόμος Newmann
4ο κεφ	ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
	Συχνότητα f
	ω η κυκλική συχνότητα (γωνιακή ταχύτητα), Τ η περίοδος και f η συχνότητα.
Αν την to =0 είναι y=0 και υ>0 τότε:	Εξισώσεις κίνησης Γ.Α.Τ
y = yoημωt	Εξίσωση απομάκρυνσης
υ = υoσυνωt όπου υo = ωyo	Εξίσωση ταχύτητας
α = -αoημωt όπου αo = ω^2 yo	Εξίσωση επιτάχυνσης
	Περίοδος
D= m ω^2	Σταθερά επαναφοράς
ΣF = m α ΣF = -m αoημωt ΣF = -m ω^2 yo ημωt ΣF = -m ω^2 y ΣF = - D y	Δύναμη επαναφοράς Ικανή και αναγκαία συνθήκη για ΑΑΤ (για σύστημα ελατήριο-σώμα ισχύει D=k)
	Κινητική ενέργεια ταλάντωσης
	Δυναμική ενέργεια ταλάντωσης
ΕΤ = Κ + U =σταθερό ΕΤ = Κmax = Umax όπου	Ενέργεια ταλάντωσης
	Απλό μαθηματικό εκκρεμές